2024-4-27 力扣刷题记录

198. 打家劫舍

#动态规划

思路分析

题目要求不能连着偷，那么在递归中可以考虑各种路线中，在当前 i 位置时是去前-1个值更好，还是取前-2个值加当前 i 值更好
写出状态转移方程

dfs[i] = max(dfs(i-1), dfs(i-2) + nums[i])

我们可以将选的过程画成一颗二叉树，如下，其中0-4表示的是 i 的值，选与不选表示的是是否选择4这个节点

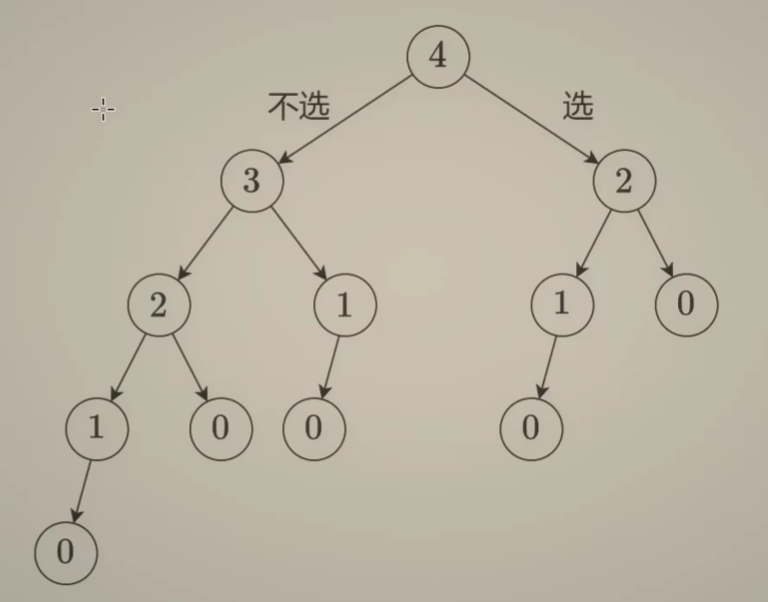
代码如下

java
import java.util.*;

class Solution {
    private int[] nums;

    public int rob(int[] nums) {
        this.nums = nums;
        int n = nums.length;
        return dfs(n - 1);
    }

    /**
     * 递归遍历房子
     * 
     * @param i
     * @return
     */
    private int dfs(int i) {
        // 如果i<0表示没有房子可选了，直接返回0
        if (i < 0) {
            return 0;
        }
        // 使用状态转移方程表示获取的最大值
        /*
         * dfs(i-1)表示在当前位置i不选，因为 “如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。”
         * dfs(i - 2) + nums[i] 表示在当前位置i选
         * 使用max则可选出这两种操作哪种得到的值最大
         */
        int res = Math.max(dfs(i - 1), dfs(i - 2) + this.nums[i]);
        return res;
    }
}

显然，答案超时了，我们需要优化代码，我们注意到搜索树，它有一些重复的地方，我们可以进行剪枝操作

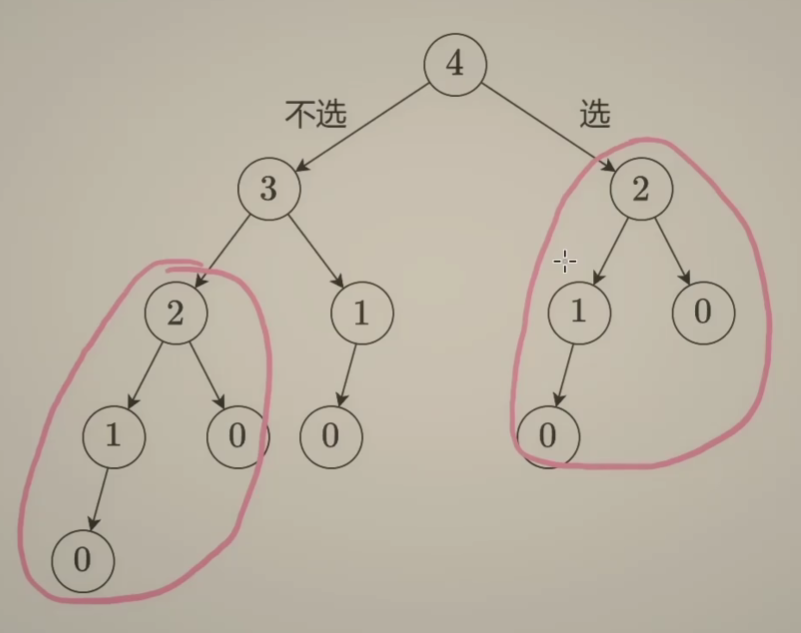
优化一

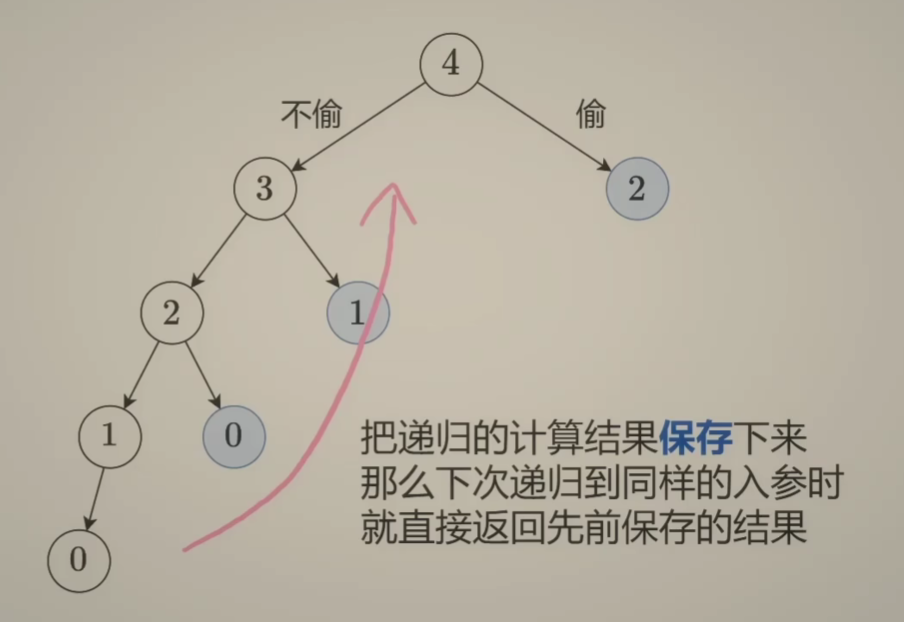
我们使用一个 memo 数组记录每次计算的值，然后在递归中判断是否进行过计算，如果 memo 数组中有值，则直接返回

java
import java.util.*;

class Solution {
    private int[] nums;
    private int[] memo;

    public int rob(int[] nums) {
        this.nums = nums;
        int n = nums.length;
        this.memo = new int[n];
        Arrays.fill(this.memo, -1);
        return dfs(n - 1);
    }

    /**
     * 递归遍历房子
     * 
     * @param i
     * @return
     */
    private int dfs(int i) {
        // 如果i<0表示没有房子可选了，直接返回0
        if (i < 0) {
            return 0;
        }
        // 如果当前值计算过了，那么直接返回
        if (this.memo[i] != -1) {
            return this.memo[i];
        }
        // 使用状态转移方程表示获取的最大值
        /*
         * dfs(i-1)表示在当前位置i不选，因为 “如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。”
         * dfs(i - 2) + nums[i] 表示在当前位置i选
         * 使用max则可选出这两种操作哪种得到的值最大
         */
        int res = Math.max(dfs(i - 1), dfs(i - 2) + this.nums[i]);
        this.memo[i] = res;
        return res;
    }
}

这样算法的复杂度就优化到了 $O(n)$

优化二

对于剪枝后的搜索树，我们还可以将其转为递推的方式
由于我们知道每个数它的前一个数应该是多少，因此我们可以直接从0开始计算

代码如下

java
import java.util.*;

class Solution {
    public int rob(int[] nums) {
        int n = nums.length;
        int[] f = new int[n + 2];
        for (int i = 0; i < n; i++) {
            f[i + 2] = Math.max(f[i + 1], f[i] + nums[i]);
        }
        return f[n - 1 + 2];
    }
}

此时的时间复杂度是 $O(n)$ ，空间复杂度也是 $O(n)$

优化三

对于 f 数组，我们知道 $当前=max(上一个+上上一个+nums[i])$
于是我们可以将 f 数组改成三个变量即可

newF = max(f_{1}, f_{0}+nums[i])

计算完后更新 $f_{1}$ 和 $f_{0}$ 即可

\begin{align} f_{0}&=f_{1} \\ f_{1}&=newF \end{align}

代码如下

java
import java.util.*;

class Solution {
    public int rob(int[] nums) {
        int n = nums.length;
        int f0 = 0, f1 = 0, newF = 0;
        for (int i = 0; i < n; i++) {
            newF = Math.max(f1, f0 + nums[i]);
            f0 = f1;
            f1 = newF;
        }
        return newF;
    }
}

这时的事件复杂度是 $O(n)$ ，空间复杂度就是 $O(1)$ 了

494. 目标和

#动态规划 #0-1背包问题

494. 目标和 - 力扣（LeetCode）

得到 0-1背包 代码

java
class Solution {
    private int[] w;
    private int[] v;
    private int[] memo;

    /**
     * 背包问题
     * 
     * @param capacity 背包容量
     * @param w        n个物品的体积
     * @param v        n个物品的价值
     * @return 所选物品在不超过capacity的情况下的最大价值
     */
    private int zeroOneKnapsack(int capacity, int[] w, int[] v) {
        int n = w.length;
        this.w = w;
        this.v = v;
        this.memo = new int[n];
        Arrays.fill(this.memo, -1);
        return dfs(n - 1, capacity);
    }

    /**
     * 遍历
     * 
     * @param i 第i个元素
     * @param c 背包容量
     * @return
     */
    private int dfs(int i, int c) {
        if (i < 0) {
            return 0;
        }
        if (this.memo[i] != -1) {
            return this.memo[i];
        }
        if (c < this.w[i]) {
            return dfs(i - 1, c);
        }
        // 选(dfs(i - 1, c - this.w[i]) + this.v[i])或者不选(dfs(i - 1, c))
        int res = Math.max(dfs(i - 1, c), dfs(i - 1, c - this.w[i]) + this.v[i]);
        this.memo[i] = res;
        return res;
    }
}

目标和思路分析

设 $p$ 为所有+号的数之和，那么 $(s-p)$ 就是所有-号的数之和
可得

\begin{align} p-(s-p)&=target \\ 2p&=target+s \\ p&=\frac{target+s}{2} \end{align}

变成了规定 target 求 p 的动态规划代码

java
import java.util.*;

class Solution {
    private int[] nums;
    private int[][] memo;

    public int findTargetSumWays(int[] nums, int target) {
        // p: nums中的+数
        // ng: s-p nums中的-数 注意，这里不是负数，而是不带-的数的和
        // 可得 p-(s-p)=target
        // 2p=target+s
        // p=(target+s)/2 我们需要求p，计算哪些条件下p是可以满足的
        // (target+s)为偶数 且不为负数(为什么要判断是否为负数，因为target可能为负数，而sum+target可能小于0，则不可能取得结果)
        this.nums = nums;
        target += Arrays.stream(nums).sum();
        if (target < 0 || (target % 2 == 1)) {
            return 0;
        }
        // 除以2去计算p
        target /= 2;

        // 01背包
        int n = nums.length;
        this.memo = new int[n][target + 1];
        for (int i = 0; i < n; i++) {
            Arrays.fill(this.memo[i], -1);
        }
        return dfs(n - 1, target);
    }

    /**
     * 遍历
     * 
     * @param i 第i个元素
     * @param c 背包容量
     * @return
     */
    private int dfs(int i, int c) {
        if (i < 0) {
            // c == 0表示这些数加起来等于target
            if (c == 0) {
                return 1; // 表示这组合可以 返回1
            }
            // c != 0 表示这些数加起来不等于target
            if (c != 0) {
                return 0; // 表示这组合不行 返回0
            }
        }
        if (this.memo[i][c] != -1) {
            return this.memo[i][c];
        }
        if (c < this.nums[i]) {
            return dfs(i - 1, c);
        }
        // 这里计算了
        int res = dfs(i - 1, c) + dfs(i - 1, c - this.nums[i]);
        this.memo[i][c] = res;
        return res;
    }
}

目录

198. 打家劫舍

494. 目标和