1 两数之和

#哈希表 #暴力解法

1. 两数之和 - 力扣（LeetCode）

1. 暴力解法

java
class Solution {
    public int[] twoSum(int[] nums, int target) {
        Integer n = nums.length;
        for (Integer i=0;i<n;i++) {
            for (Integer j=i+1;j<n;j++) {
                if (nums[i] + nums[j] == target) {
                    return new int[]{i,j};
                }
            }
        }
        return new int[0];
    }
}

只需要两层嵌套循环遍历所有数即可

复杂度分析

• 时间复杂度: $O(n^2)$，其中 $n$ 为 $nums$ 的长度
• 空间复杂度：$O(1)$

2. 哈希表解法

java
class Solution {
    public int[] twoSum(int[] nums, int target) {
        Integer n = nums.length;
        Map<Integer, Integer> hashMap = new HashMap<>(n-1); // 创建哈希表，初始化的话可以减少性能损失
        hashMap.put(nums[0], 0); // 将第一个数先放入哈希表
        for (int i=1;i<n;i++) {
            if (hashMap.containsKey(target - nums[i])) {
                return new int[]{hashMap.get(target - nums[i]), i}; // 如果包含第二个数，则从哈希表中取出键值
            }
            hashMap.put(nums[i],i); // 不符合则放入哈希表中
        }
        return new int[0];
    }
}

复杂度分析

• 时间复杂度: $O(n)$，其中 $n$ 为 $nums$ 的长度
• 空间复杂度：$O(n)$，哈希表中需要多存 $n-1$ 个键值对

167. 两数之和 II - 输入有序数组

#双指针

167. 两数之和 II - 输入有序数组 - 力扣（LeetCode）

1. 暴力解法

和 I 一样的暴力解法是会超过时间限制的，所以需要其他方法

复杂度分析

• 时间复杂度：$O(n^2)$
• 空间复杂度: $O(1)$

2. 双指针

因为数组为递增数组，所以当数组 $nums[0] + nums[len-1] < target$ 就应该寻找大一些的组合 即 $nums[1]+nums[len-1]$ 如果 $nums[0] + nums[len-1] > target$，那么应该找小一些的组合 即

由此得到应该有两个左右的指针在移动

java
class Solution {
    // TODO
    public int[] twoSum(int[] nums, int target) {
        int l = 0;
        int r = nums.length - 1;
        while (l < r) { // 或者 true 题目默认 left < right
            int s = nums[l] + nums[r];
            if (s == target) {
                break;
            }
            if (s > target) {
                r -= 1;
            } else {
                l += 1;
            }
        }
        return new int[] { l + 1, r + 1 };
    }
}

复杂度分析

• 空间复杂度：只使用了一个常数个变量，所以复杂度为 $O(1)$
• 时间复杂度：一层 while 循环，因此复杂度为 $O(n)$

2824. 统计和小于目标的下标对数目

#双指针

2824. 统计和小于目标的下标对数目 - 力扣（LeetCode）

该题的前置题是167

相向双指针思路

• 为什么可以排序呢？题目相当于从数组中选两个数，我们只关心这两个数的和是否小于 $target$，由于 $a+b=b+a$ ，无论如何排列数组元素，都不会影响加法的结果，所以排序不影响答案。
• 排序后：
  • 初始化左右指针 $left=0,right=n−1$。
  • 如果 $nums[left]+nums[right]<target$，由于数组是有序的，$nums[left]$ 与下标 $i$ 在 $[left+1,right]$ 中的任何 $nums[i]$ 相加，都是 $<target$ 的，因此直接找到了 $right−left$ 个合法数对，加到答案中，然后将 $left$ 加一。
  • 如果 $nums[left]+nums[right]≥target$，由于数组是有序的，$nums[right]$ 与下标 $i$ 在 $[left,right−1]$ 中的任何 $nums[i]$ 相加，都是 $≥target$ 的，因此后面无需考虑 $nums[right]$，将 $right$ 减一。
  • 重复上述过程直到 $left≥right$ 为止。

java
import java.util.Collections;
import java.util.List;

class Solution {
    public int countPairs(List<Integer> nums, int target) {
        int n = nums.size();
        // 排序，因为只要求返回数组个数，对于顺序没有要求
        Collections.sort(nums);
        int ans = 0;
        int left = 0;
        int right = n - 1;
        // 遍历
        while (left < right) {
            // nums[left] + nums[right] < target 则 left到right中间的数都小于target
            if (nums.get(left) + nums.get(right) < target) {
                ans += right - left;
                left++;
                // 否则的话，移动right，再判断nums[left] + nums[right] < target
            } else {
                right--;
            }
        }
        return ans;
    }
}

复杂度分析

• 时间复杂度: $O(n\log n)$，其中 $n$ 为 $nums$ 的长度。瓶颈在排序上。
• 空间复杂度：$O(1)$

15. 三数之和

#双指针

15. 三数之和 - 力扣（LeetCode）

1. 相向双指针

类似于两数之和 II 中的 num[i]+num[j]=target，这个也可以转换为这种

于是可得

java
import java.util.*;

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        Arrays.sort(nums); // 排序之后使用双指针进行查找
        // 本体思路和两数之和II相似
        // 将nums[i] + nums[j] + nums[k] == 0转化为num[j] + nums[k] = nums[i]即可
        List<List<Integer>> ans = new ArrayList<List<Integer>>();
        int n = nums.length;
        for (int i = 0; i < n - 2; i++) {
            if (i > 0 && nums[i] == nums[i - 1]) {
                continue;// 如果和它上一个数相同，则跳过
            }
            
            // *优化*
            // 如果nums[i] + nums[i+1] + nums[i+2] > 0代表nums[i] + 后面任意数都大于0，因此没有结果
            if (nums[i] + nums[i + 1] + nums[i + 2] > 0) {
                break;
            }
            // 如果nums[i]和最后两个数相加 < 0代表nums[i]和后面任意数相加都小于0，因此跳过这个数，后面的nums[i]可能会变大
            if (nums[i] + nums[n - 1] + nums[n - 1 - 1] < 0) {
                continue;
            }
            
            int j = i + 1; // 在i到nums数组末尾左右分别两个指针
            int k = n - 1;
            while (j < k) {
                int s = nums[i] + nums[j] + nums[k];
                if (s > 0) {
                    k -= 1;// k向左移，让总和变小
                } else if (s < 0) {
                    j += 1; // j向右移动，让综合变大
                } else {
                    // 这个时候得到的就是结果了
                    ans.add(Arrays.asList(nums[i], nums[j], nums[k]));
                    // 内层双指针的跳过方式也一样
                    j += 1;
                    while (j < k && nums[j] == nums[j - 1]) {
                        j += 1;
                    }
                    k -= 1;
                    while (k > j && nums[k] == nums[k + 1]) {
                        k -= 1;
                    }
                }
            }
        }
        return ans;
    }
}

优化

• 如果 $nums[i] + nums[i+1] + nums[i+2] > 0$ 代表 $nums[i]$ + 后面任意数都大于0，因此没有结果
• 如果 $nums[i]$ 和最后两个数相加 < 0代表 $nums[i]$ 和后面任意数相加都小于0，因此跳过这个数，后面的 $nums[i]$ 可能会变大

java
// *优化*
// 如果nums[i] + nums[i+1] + nums[i+2] > 0代表nums[i] + 后面任意数都大于0，因此没有结果
if (nums[i] + nums[i + 1] + nums[i + 2] > 0) {
	break;
}
// 如果nums[i]和最后两个数相加 < 0代表nums[i]和后面任意数相加都小于0，因此跳过这个数，后面的nums[i]可能会变大
if (nums[i] + nums[n - 1] + nums[n - 1 - 1] < 0) {
	continue;
}

复杂度分析

• 时间复杂度：两层循环，所以是 $O(n^2)$
• 空间复杂度：由于没有使用额外的变量，所以的 $O(1)$

16. 最接近的三数之和

#双指针

16. 最接近的三数之和 - 力扣（LeetCode）

双指针思路

• 思路和 15. 三数之和 类似，排序后，枚举 $nums[i]$ 作为第一个数，那么问题变成找到另外两个数，使得这三个数的和与 $target$ 最接近，这同样可以用双指针解决。 设 $s=nums[i]+nums[j]+nums[k]$，为了判断 $s$ 是不是与 $target$ 最近的数，我们还需要用一个变量 $minDiff$ 维护 $∣s−target∣$ 的最小值。分类讨论：
• 如果$s=target$，那么答案就是 $s$，直接返回 $s$。
• 如果 $s>target$，那么如果 $s−target<minDiff$，说明找到了一个与 $target$ 更近的数，更新 $minDiff$ 为 $s−target$，更新答案为 $s$。然后和三数之和一样，把 $k$ 减一。
• 否则 $s<target$，那么如果 $target−s<minDiff$，说明找到了一个与 $target$ 更近的数，更新 $minDiff$ 为 $target−s$，更新答案为 $s$。然后和三数之和一样，把 $j$ 加一。 除此以外，还有以下几个优化：

1. 设 $s=nums[i]+nums[i+1]+nums[i+2]$。如果 $s>target$，由于数组已经排序，后面无论怎么选，选出的三个数的和不会比 $s$ 还小，所以不会找到比 $s$ 更优的答案了。所以只要 $s>target，就可以直接 `break` 外层循环了。在 `break` 前判断$s$是否离$target$更近，如果更近，那么更新答案为$s$。
2. 设 $s=nums[i]+nums[n−2]+nums[n−1]$。如果 $s<target$，由于数组已经排序，$nums[i]$ 加上后面任意两个数都不超过 $s$，所以下面的双指针就不需要跑了，无法找到比 $s$ 更优的答案。但是后面还有更大的 $nums[i]$，可能找到一个离 $target$ 更近的三数之和，所以还需要继续枚举，continue 外层循环。在 continue 前判断 $s$ 是否离 $target$ 更近，如果更近，那么更新答案为 $s$，更新 $minDiff$为 $target−s$。
3. 如果 $i>0$ 且$nums[i]=nums[i−1]$，那么 $nums[i]$ 和后面数字相加的结果，必然在之前算出过，所以无需跑下面的双指针，直接 continue 外层循环。（可以放在循环开头判断。）

java
import java.util.*;

class Solution {
    public int threeSumClosest(int[] nums, int target) {
        Arrays.sort(nums); // 思路和三数之和一样，先排序
        int n = nums.length;
        int ans = 0;
        int minDiff = Integer.MAX_VALUE; // 最小的差值
        for (int i = 0; i < n - 2; i++) {
            // *优化*
            // 优化三：如果nums[i]==nums[i-1]，那么在i-1时已经算过所有i时的数，所以直接跳过
            if (i >= 1 && nums[i] == nums[i - 1]) {
                continue;
            }
            // 优化一：如果nums[i] + nums[i+1] + nums[i+2] > target 那么之后的所有数都不会比他们的和更接近target
            int s = nums[i] + nums[i + 1] + nums[i + 2];
            if (s > target) {
                // 如果是最小差值，更新ans
                if (s - target < minDiff) {
                    ans = s;
                }
                break;
            }
            // 优化二：如果nums[i] + nums[n-2] + nums[n-1] < target 那么之前的所有数都不会比他们的和更接近target
            s = nums[i] + nums[n - 2] + nums[n - 1];
            if (s < target) {
                // 如果是最小差值，更新ans和minDiff
                if (target - s < minDiff) {
                    minDiff = target - s;
                    ans = s;
                }
                continue; // 但是i之后的数可能还有更接近target的，所以continue
            }

            // 双指针
            int j = i + 1;// 在i到nums数组末尾左右分别两个指针
            int k = n - 1;
            while (j < k) {
                // 如果相等，直接返回
                s = nums[i] + nums[j] + nums[k];
                if (s == target) {
                    return target;
                }
                // 判断是否和target差距最小
                if (s > target) {
                    if (s - target < minDiff) { // s与target更接近
                        minDiff = s - target;
                        ans = s; // 存入ans中，当下次查找到更小的minDiff时更新
                    }
                    k--; // 数组经过排序，数值由小到大，因此s > target时寻找更小的值需要右指针k向左移动
                }
                if (s < target) {
                    if (target - s < minDiff) { // s与target更接近
                        minDiff = target - s;
                        ans = s; // 存入ans中，当下次查找到更小的minDiff时更新
                    }
                    j++; // 数组经过排序，数值由小到大，因此s < target时寻找更小的值需要左指针j向左移动
                }
            }
        }
        return ans;
    }
}

复杂度分析

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(1)$

18. 四数之和

#双指针

18. 四数之和 - 力扣（LeetCode）

双指针思路 思路和 15. 三数之和 一样，排序后，枚举 $nums[a]$ 作为第一个数，枚举$nums[b]$作为第二个数，那么问题变成找到另外两个数，使得这四个数的和等于 $target$，这可以用双指针解决。

优化思路也和视频中讲的一样，对于 $nums[a]$ 的枚举：

1. 设 $s=nums[a]+nums[a+1]+nums[a+2]+nums[a+3]$。如果 $s>target$ ，由于数组已经排序，后面无论怎么选，选出的四个数的和不会比 $s$ 还小，所以后面不会找到等于$target$ 的四数之和了。所以只要 $s>targets$，就可以直接 break 外层循环了。
2. 设 $s=nums[a]+nums[n−3]+nums[n−2]+nums[n−1]$。如果 $s<target$ ，由于数组已经排序，$nums[a]$ 加上后面任意三个数都不会超过 $s$，所以无法在后面找到另外三个数与 $nums[a]$ 相加等于 $target$。但是后面还有更大的 $nums[a]$，可能出现四数之和等于 $target$ 的情况，所以还需要继续枚举，continue 外层循环。
3. 如果 $a>0$ 且 $nums[a]=nums[a−1]$，那么 $nums[a]$ 和后面数字相加的结果，必然在之前算出过，所以无需执行后续代码，直接 continue 外层循环。（可以放在循环开头判断。） 对于 $nums[b]$ 的枚举（$b$ 从 $a+1$ 开始），也同样有类似优化：
4. 设 $s=nums[a]+nums[b]+nums[b+1]+nums[b+2]$。如果 $s>target$ ，由于数组已经排序，后面无论怎么选，选出的四个数的和不会比 $s$ 还小，所以后面不会找到等于 $target$ 的四数之和了。所以只要 $s>targets$，就可以直接 break。
5. 设 $s=nums[a]+nums[b]+nums[n−2]+nums[n−1]$。如果 $s<target$ ，由于数组已经排序，$nums[a]+nums[b]$ 加上后面任意两个数都不会超过 $s$，所以无法在后面找到另外两个数与 $nums[a]$ 和 $nums[b]$ 相加等于 $target$。但是后面还有更大的 $nums[b]$，可能出现四数之和等于 $target$ 的情况，所以还需要继续枚举，continue。
6. 如果 $b>a+1$  且 $nums[b]=nums[b−1]$，那么 $nums[b]$ 和后面数字相加的结果，必然在之前算出过，所以无需执行后续代码，直接 continue。注意这里 $b>a+1$ 的判断是必须的，如果不判断，对于示例 2 这样的数据，会直接 continue，漏掉符合要求的答案。 对于 Java、C++ 等语言，注意相加结果可能会超过 323232 位整数范围，需要用 646464 位整数存储四数之和。

java
import java.util.*;

class Solution {
    public List<List<Integer>> fourSum(int[] nums, int target) {
        // 排序
        Arrays.sort(nums);
        // 思路和三数之和一样，但是需要枚举两次
        int n = nums.length;
        List<List<Integer>> ans = new ArrayList<>();
        for (int a = 0; a < n - 3; a++) { // 这里-3是因为需要留出3个数
            long x = nums[a];
            if (a > 0 && x == nums[a - 1])
            continue; // 跳过重复数字
            // *优化*
            if (x + nums[a + 1] + nums[a + 2] + nums[a + 3] > target)
            break; // 优化一
            if (x + nums[n - 3] + nums[n - 2] + nums[n - 1] < target)
            continue; // 优化二
            for (int b = a + 1; b < n - 2; b++) { // b=a+1 a左边的不需要看了 -2和上面一样
                long y = nums[b];
                if (b > a + 1 && y == nums[b - 1])
                continue; // 跳过重复数字
                // *优化*
                if (x + y + nums[b + 1] + nums[b + 2] > target)
                break; // 优化一
                if (x + y + nums[n - 2] + nums[n - 1] < target)
                continue; // 优化二
                int c = b + 1;
                int d = n - 1;
                while (c < d) {
                    long s = x + y + nums[c] + nums[d];
                    if (s > target) {
                        d--; // 大于target让右指针左移
                    }
                    if (s < target) {
                        c++; // 小于target让左指针右移
                    }
                    if (s == target) {
                        ans.add(Arrays.asList((int) x, (int) y, nums[c], nums[d]));
                        // 跳过重复数字
                        c += 1;
                        while (c < d && nums[c] == nums[c - 1]) {
                            c += 1;
                        }
                        d -= 1;
                        while (d > c && nums[d] == nums[d + 1]) {
                            d -= 1;
                        }
                    }
                }
            }
        }
        return ans;
    }
}

复杂度分析

• 时间复杂度：三层循环 $O(n^3)$
• 空间复杂度：$O(1)$

611. 有效三角形的个数

#双指针

611. 有效三角形的个数 - 力扣（LeetCode）

双指针思路

从 $nums$ 中选三个数，满足 $1≤a≤b≤c$且 $a+b>c$ 的方案数 为了能够使用相向双指针，先对数组从小到大排序。 外层循环枚举 $c=nums[k]$，内层循环用相向双指针枚举 $a=nums[i]$ 和 $b=nums[j]$，具体如下：

• 初始化左右指针 $i=0,j=k−1$。
• 如果 $nums[i]+nums[j]>c$，由于数组是有序的，$nums[j]$ 与下标 $i′$ 在 $[i,j−1]$ 中的任何 $nums[i′]$ 相加，都是 $>c$ 的，因此直接找到了 $j−i$ 个合法方案，加到答案中，然后将 $j$ 减一。
• 如果 $nums[i]+nums[j]≤c$，由于数组是有序的，$nums[i]$ 与下标 $j′$ 在 $[i+1,j] 中的任何$nums[j′]$相加，都是$≤c$的，因此后面无需考虑$nums[i]$，将$i$ 加一。
• 重复上述过程直到 $i≥j$ 为止。

java
import java.util.*;

class Solution {
    public int triangleNumber(int[] nums) {
        // 排序
        Arrays.sort(nums);
        int ans = 0;
        for (int k = 2; k < nums.length; ++k) {
            int c = nums[k];
            int i = 0; // a=nums[i]
            int j = k - 1; // b=nums[j]
            // 在k左右两边的双指针i、j
            while (i < j) {
                if (nums[i] + nums[j] > c) {
                    // 由于 nums 已经从小到大排序
                    // nums[i]+nums[j] > c 同时意味着：
                    // nums[i+1]+nums[j] > c
                    // nums[i+2]+nums[j] > c
                    // ...
                    // nums[j-1]+nums[j] > c
                    // 从 i 到 j-1 一共 j-i 个
                    ans += j - i;
                    j--;
                } else {
                    // 由于 nums 已经从小到大排序
                    // nums[i]+nums[j] <= c 同时意味着
                    // nums[i]+nums[j-1] <= c
                    // ...
                    // nums[i]+nums[i+1] <= c
                    // 所以在后续的循环中，nums[i] 不可能作为三角形的边长，没有用了
                    i++;
                }
            }
        }
        return ans;
    }
}

复杂度分析

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(1)$

11. 盛最多水的容器

#双指针

11. 盛最多水的容器 - 力扣（LeetCode）

1. 双指针

java
class Solution {
    public int maxArea(int[] height) {
        int ans = 0;
        int left = 0;
        int right = height.length - 1;
        while (left < right) {
            int area = (right - left) * Math.min(height[left], height[right]);
            ans = Math.max(ans, area);
            if (height[left] < height[right]) {
                left += 1;
            } else {
                right -= 1;
            }
        }
        return ans;
    }
}

复杂度分析

• 时间复杂度：使用一层循环，为 $O(n)$
• 空间复杂度：$O(1)$

42. 接雨水

#前后缀分解 #双指针

42. 接雨水 - 力扣（LeetCode）

前后缀分解思路分析

• 使用前缀后缀最小值减去高度，得到每个单位的盛水体积

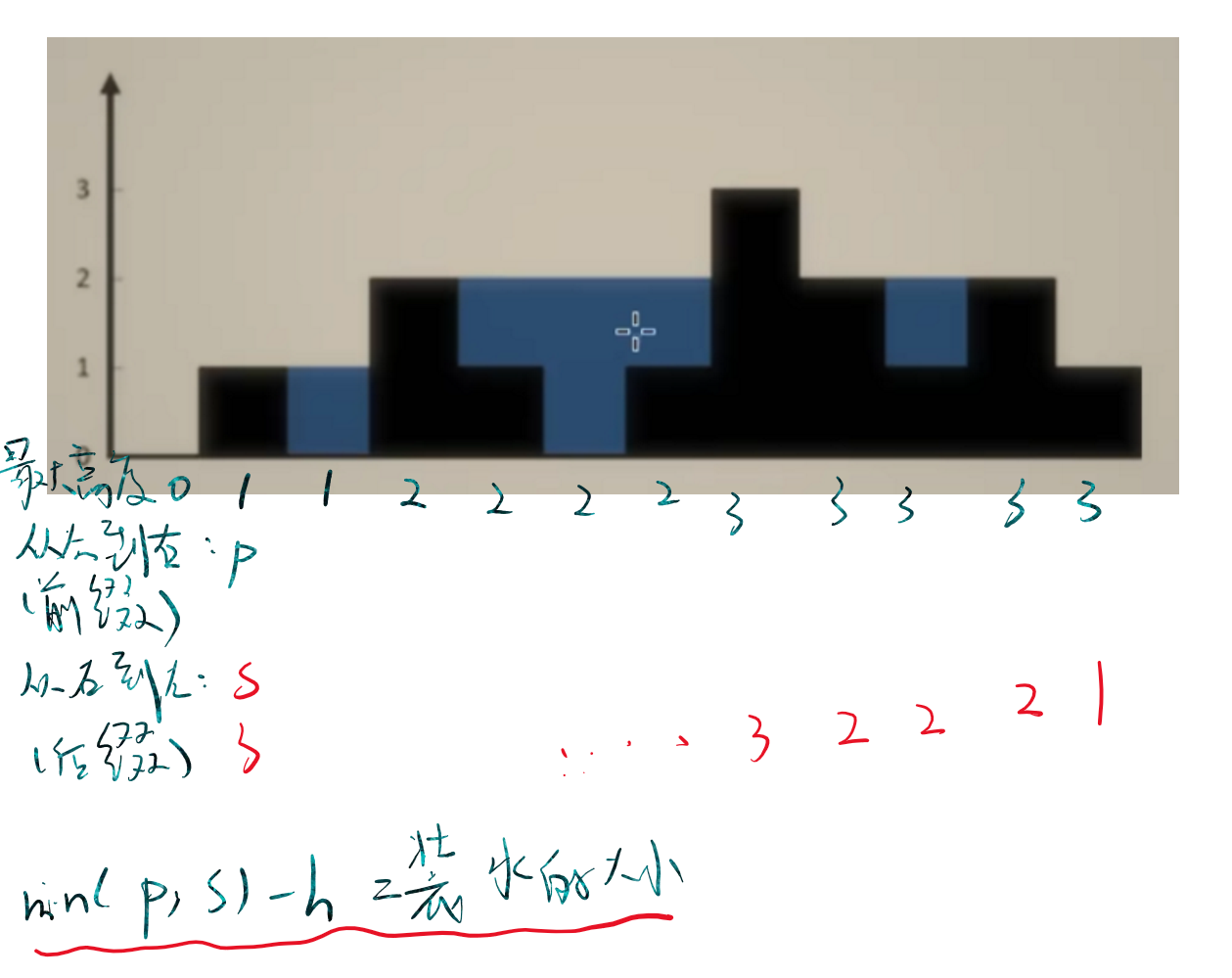
按照这个思路，写出代码

java
import java.util.*;

class Solution {
    public int trap(int[] height) {
        int n = height.length;
        // 计算前缀最大值
        int[] pre_max = new int[n];
        pre_max[0] = height[0]; // 前缀的第一项为高度数组的第一项
        // 遍历数组，取最大值
        for (int i = 1; i < n; i++) {
            pre_max[i] = Math.max(pre_max[i - 1], height[i]);
        }
        // 计算后缀最大值
        int[] suf_max = new int[n];
        suf_max[n - 1] = height[n - 1];
        // 遍历数组，取最大值
        for (int i = n - 1 - 1; i >= 0; i--) {
            suf_max[i] = Math.max(suf_max[i + 1], height[i]);
        }
        // 计算答案
        int ans = 0;
        for (int i = 0; i < n; i++) {
            ans += Math.min(pre_max[i], suf_max[i]) - height[i];
        }
        return ans;
    }
}

复杂度分析

• 时间复杂度：$O(n)$ 都是一层循环
• 空间复杂度：$O(n)$ 使用了两组额外的数组

双指针前后缀分解思路分析

• 使用两个指针在前后移动不需要使用数组，可减小空间复杂度，同时减少了循环次数，也一定程度上减少了时间

代码

java
import java.util.*;

class Solution {
    public int trap(int[] height) {
        int n = height.length;
        int ans = 0;
        int left = 0;
        int right = n - 1;
        int pre_max = 0;
        int suf_max = 0;
        // 通过移动指针计算前缀和后缀最大值
        while (left <= right) {
            pre_max = Math.max(pre_max, height[left]);
            suf_max = Math.max(suf_max, height[right]);
            // 这里和之前的方法一样，都是使用最小值和height相减得到该位置的水体积
            if (pre_max < suf_max) {
                ans += pre_max - height[left];
                left += 1;
            }else {
                ans += suf_max - height[right];
                right --;
            }
        }
        return ans;
    }
}

复杂度分析

• 时间复杂度：$O(n)$
• 空间复杂度：由于没有使用额外数组变量，故空间复杂度为 $O(1)$